Advertisements
Advertisements
प्रश्न
Show that the ∆ABC is an isosceles triangle if the determinant
Δ = `[(1, 1, 1),(1 + cos"A", 1 + cos"B", 1 + cos"C"),(cos^2"A" + cos"A", cos^2"B" + cos"B", cos^2"C" + cos"C")]` = 0
उत्तर
We have, Δ = `[(1, 1, 1),(1 + cos"A", 1 + cos"B", 1 + cos"C"),(cos^2"A" + cos"A", cos^2"B" + cos"B", cos^2"C" + cos"C")]` = 0
[Applying C1 → C1 – C2 and C2 → C2 – C3]
⇒ `[(0, 0, 1),(cos"A" - cos"C", cos"B" - cos"C", 1 + cos"C"),(cos^2"A" + cos"A" - cos^2"C" - cos"C", cos^2"B" + cos"B" - cos^2"C" - cos"C", cos^2"C" + cos"C")]` = 0
[Taking (cos A – cos C) common from C1 and (cos B – cos C) common from C2]
⇒ `(cos "A" - cos "C") (cos "B" - cos "C") xx [(0, 0, 1),(1, 1, 1 + cos"C"),(cos"A" + cos"C" + 1, cos"B" + cos"C" + 1, cos^2"C" + cos"C")]` = 0
[Applying C1 → C1 – C2]
⇒ `(cos "A" - cos "C") (cos "B" - cos "C") xx [(0, 0, 1),(0, 1, 1 + cos"C"),(cos"A" - cos"B", cos"B" + cos"C" + 1, cos^2"C" + cos"C")]` = 0
⇒ `(cos"A" - cos"C")(cos"B" - cos"C")(cos"B" - cos"A")` = 0
⇒ cos A = cos C or cos B = cos C or cos B = cos A
⇒ A = C or B = C or B = A
Hence, ΔABC is an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
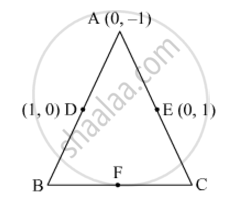
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
If the points A(−2, 1), B(a, b) and C(4, −1) are collinear and a − b = 1, find the values of a and b.
If P(–5, –3), Q(–4, –6), R(2, –3) and S(1, 2) are the vertices of a quadrilateral PQRS, find its area.
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
In each of the following find the value of 'k', for which the points are collinear.
(7, -2), (5, 1), (3, -k)
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).
Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
Four points A (6, 3), B (−3, 5), C(4, −2) and D (x, 3x) are given in such a way that `(ΔDBG) /(ΔABG)=1/2,` find x
If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA2+ PB2 + PC2 = GA2 + GB2 + GC2 + 3GP2.
If the coordinates of the mid-points of the sides of a triangle are (1, 1), (2, —3) and (3, 4), find the vertices of the triangle.
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm ?
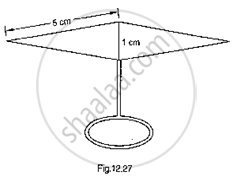
Find the area of the blades of thc magnetic compass shown in Fig.. 12.27. (Take √11 = 3.32).
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
Find the area of ΔABC with A(1, -4) and midpoints of sides through A being (2, -1) and (0, -1).
Find the value of y for which the points A(-3, 9), B(2,y) and C(4,-5) are collinear.
Find a relation between x and y, if the points A(2, 1), B(x, y) and C(7,5) are collinear.
Find the area of ΔABC with vertices A(0, -1), B(2,1) and C(0, 3). Also, find the area of the triangle formed by joining the midpoints of its sides. Show that the ratio of the areas of two triangles is 4:1.
Using integration, find the area of the triangle whose vertices are (2, 3), (3, 5) and (4, 4).
Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.

In a triangle ABC, if `|(1, 1, 1),(1 + sin"A", 1 + sin"B", 1 + sin"C"),(sin"A" + sin^2"A", sin"B" + sin^2"B", sin"C" + sin^2"C")|` = 0, then prove that ∆ABC is an isoceles triangle.
Points A(3, 1), B(12, –2) and C(0, 2) cannot be the vertices of a triangle.
Find the value of m if the points (5, 1), (–2, –3) and (8, 2m) are collinear.
If `D((-1)/2, 5/2), E(7, 3)` and `F(7/2, 7/2)` are the midpoints of sides of ∆ABC, find the area of the ∆ABC.
The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
The area of a triangle with base 4 cm and height 6 cm is 24 cm2.
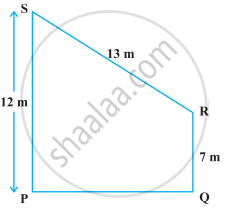
Find the area of the trapezium PQRS with height PQ given in the following figure.
The area of a trapezium is 475 cm2 and the height is 19 cm. Find the lengths of its two parallel sides if one side is 4 cm greater than the other.
Using determinants, find the area of ΔPQR with vertices P(3, 1), Q(9, 3) and R(5, 7). Also, find the equation of line PQ using determinants.
