Advertisements
Advertisements
प्रश्न
Show that the points (a + 5, a – 4), (a – 2, a + 3) and (a, a) do not lie on a straight line for any value of a.
उत्तर
Given, the points are (a + 5, a – 4), (a – 2, a + 3) and (a, a).
We have to prove that these pints do not lie on a straaighine.
So, we have to prove that these points form a triangle.
Area, Δ = `1/2|("a" + 5, "a" - 4, 1),("a" - 2, "a" + 3, 1),("a", "a", 1)|`
[Applying R1 → R1 – R3 and R2 → R2 – R3]
= `1/2 |(5, -4, 0),(-2, 3, 0),("a", "a", 1)|`
= `1/2[(1 * (15 - 8)]`
= `7/2 ≠ 0`
Hence, given points from a triangle i.e., points do not lie on a straight line.
APPEARS IN
संबंधित प्रश्न
If the points A(x, 2), B(−3, −4) and C(7, − 5) are collinear, then the value of x is:
(A) −63
(B) 63
(C) 60
(D) −60
If the points A(−2, 1), B(a, b) and C(4, −1) are collinear and a − b = 1, find the values of a and b.
If the points P(–3, 9), Q(a, b) and R(4, – 5) are collinear and a + b = 1, find the values of a and b.
Find the area of a triangle whose vertices are A(3, 2), B (11, 8) and C(8, 12).
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).
Find the centre of a circle passing through the points (6, − 6), (3, − 7) and (3, 3).
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
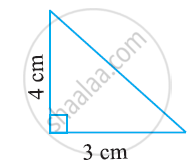
Find the area of the following triangle:
If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
Prove that the points (a, b), (a1, b1) and (a −a1, b −b1) are collinear if ab1 = a1b.
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
prove that the points A (7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right triangle.
Find the centroid of ΔABC whose vertices are A(-1, 0) B(5, -2) and C(8,2)
Show that the following points are collinear:
(i) A(2,-2), B(-3, 8) and C(-1, 4)
For what value of y, are the points P(1, 4), Q(3,y) and R(-3, 16) are collinear ?
Find the value(s) of p for which the points (3p + 1, p), (p + 2, p – 5) and (p + 1, –p) are collinear ?
The coordinates of the point P dividing the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1 are:
Find the area of the triangle whose vertices are (-2, 6), (3, -6), and (1, 5).
The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
A(6, 1), B(8, 2) and C(9, 4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ∆ADE.
The dimensions of a rectangle ABCD are 51 cm × 25 cm. A trapezium PQCD with its parallel sides QC and PD in the ratio 9 : 8, is cut off from the rectangle as shown in the following figure. If the area of the trapezium PQCD is `5/6` th part of the area of the rectangle, find the lengths QC and PD.

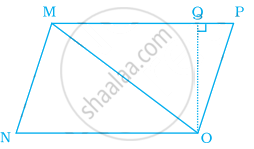
Area of triangle MNO in the figure is ______.
Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
If area of a triangular piece of cardboard is 90 cm2, then the length of altitude corresponding to 20 cm long base is ______ cm.
In the given figure, ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of ΔACD.

Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
