Advertisements
Advertisements
प्रश्न
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle
उत्तर
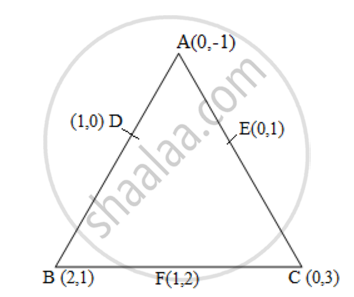
Let the vertices of the triangle be A (0, -1), B (2, 1), C (0, 3).
Let D, E, F be the mid-points of the sides of this triangle. Coordinates of D, E, and F are given by
= 1/2 {8} = 4 square units
APPEARS IN
संबंधित प्रश्न
A(4, - 6), B(3,- 2) and C(5, 2) are the vertices of a 8 ABC and AD is its median. Prove that the median AD divides Δ ABC into two triangles of equal areas.
If A(4, –6), B(3, –2) and C(5, 2) are the vertices of ∆ABC, then verify the fact that a median of a triangle ABC divides it into two triangle of equal areas.
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
Prove that the points (a, b), (a1, b1) and (a −a1, b −b1) are collinear if ab1 = a1b.
Prove analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
If the centroid of ΔABC having vertices A (a,b) , B (b,c) and C (c,a) is the origin, then find the value of (a+b+c).
Let `Delta = abs (("x", "y", "z"),("x"^2, "y"^2, "z"^2),("x"^3, "y"^3, "z"^3)),` then the value of `Delta` is ____________.
The area of ∆ABC is 8 cm2 in which AB = AC = 4 cm and ∠A = 90º.
Area of a triangle = `1/2` base × ______.
