Advertisements
Advertisements
Question
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.
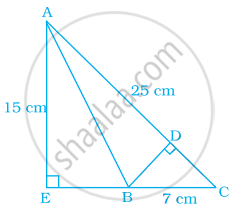
Solution
Given, AC = 25 cm, BC = 7 cm, and AE = 15 cm
In ΔAEC, using Pythagoras theorem,
AC2 = AE2 + EC2
⇒ EC2 = AC2 – AE2
⇒ EC2 = (25)2 – (15)2 = 625 – 225 = 400
EC = `sqrt(400)` = 20 cm
and EB = EC – BC = 20 – 7 = 13 cm
Area of ΔAEC = `1/2` × AE × EC
= `1/2 xx 15 xx 20`
= 150 cm2
and Area of ΔAEB = `1/2` × AE × EB
= `1/2 xx 15 xx 13`
= 97.5 cm2
∴ Area of ΔABC = Area of ΔAEC – Area of ΔAEB
= 150 – 97.5
= 52.5 cm2
Again, Area of ΔABC = `1/2` × BD × AC
52.5 = `1/2` × BD × 25
⇒ BD = `(52.5 xx 2)/25` = 4.2 cm
Hence, the area of ΔABC is 52.5 cm2 and the length of DB is 4.2 cm.
APPEARS IN
RELATED QUESTIONS
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
Prove analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
Find the value(s) of k so that the quadratic equation x2 − 4kx + k = 0 has equal roots.
Find the value of p for which the points (−5, 1), (1, p) and (4, −2) are collinear.
Show that the points (a + 5, a – 4), (a – 2, a + 3) and (a, a) do not lie on a straight line for any value of a.
Let `Delta = abs (("x", "y", "z"),("x"^2, "y"^2, "z"^2),("x"^3, "y"^3, "z"^3)),` then the value of `Delta` is ____________.
Area of triangle MNO in the figure is ______.
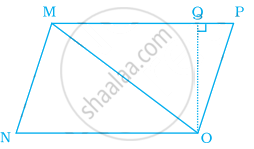
Ratio of areas of ∆MNO, ∆MOP and ∆MPQ in the given figure is ______.

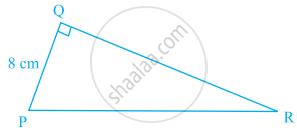
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.
If (a, b), (c, d) and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then `|(a, c, e),(b, d, f),(1, 1, 1)|^2` is equal to ______.
