Advertisements
Advertisements
Question
Prove analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
Solution
LetΔOAB be any triangle such that O is the origin and the other co-ordinates areA(x1y1):(x2,y2). P and R are the mid-points of the sides OA and OB respectively.
We have to prove that line joining the mid-point of any two sides of a triangle is equal to half of the third side which means,
`PR=1/2(AB)`
In general to find the mid-pointp(x,y) of two points `A(x_1,x_2)`and `B(x_2,y_2)` we use section formula as,
`P(x,y)=((x_1+x_2)/2,(y_1+y_2) /2)`
so,
Co-ordinates of p is,
`P(x_1/2,y_1/2)`
Similarly, co-ordinates of R is,
`R(x_2/2,y_2/2)`
In general, the distance between A`(x_1,y_1)` and B`(x_2,y_2)`is given by,
`AB=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`
Similarly,
`PR=sqrt((x_2/2-x_1/2)^2+(y_2/2-y_1/2)^2)`
`=1/2 sqrt((x_2-x_1)2+(y_2-y_1)2 `
`1/2(AB) `
Hence,
`PR=1/2(AB)`
APPEARS IN
RELATED QUESTIONS
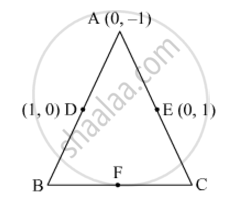
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle
The vertices of a ΔABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that `(AD)/(AB) = (AE)/(AC) = 1/4`Calculate the area of the ΔADE and compare it with the area of ΔABC. (Recall Converse of basic proportionality theorem and Theorem 6.6 related to ratio of areas of two similar triangles)
The point A divides the join of P (−5, 1) and Q(3, 5) in the ratio k:1. Find the two values of k for which the area of ΔABC where B is (1, 5) and C(7, −2) is equal to 2 units.
The area of a triangle is 5. Two of its vertices are (2, 1) and (3, −2). The third vertex lies on y = x + 3. Find the third vertex.
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 ?
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.

Area of triangle MNO in the figure is ______.