Advertisements
Advertisements
Question
Ratio of areas of ∆MNO, ∆MOP and ∆MPQ in the given figure is ______.

Options
2:1:3
1:3:2
2:3:1
1:2:3
Solution
Ratio of areas of ∆MNO, ∆MOP and ∆MPQ in the given figure is 2:1:3.
Explanation:

We know that, area of triangle = `1/2` × base × height
So, area of triangle MNO = `1/2` × NO × MO
= `1/2` × 5 × 4
= `1/2` × 20
= 10 cm2
Area of triangle MOP = `1/2` × MO × OP
= `1/2` × 5 × 2
= `1/2` × 10
= 5 cm2
Area of triangle MPQ = `1/2` × MO × PQ ......[MP = MO]
= `1/2` × 5 × 6
= `1/2` × 30
= 15 cm2
So, the ratio of area = 10:5:15 ......[Divide each by 5]
Then we get, 2:1:3
APPEARS IN
RELATED QUESTIONS
Find the area of a triangle whose vertices are A(3, 2), B (11, 8) and C(8, 12).
The vertices of ∆ABC = are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that `\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}` .Calculate the area of ∆ADE and compare it with the area of ∆ABC
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm ?
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm ?
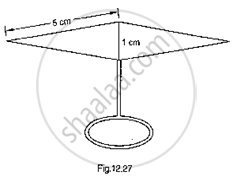
Find the area of the blades of thc magnetic compass shown in Fig.. 12.27. (Take √11 = 3.32).
Using determinants, find the values of k, if the area of triangle with vertices (–2, 0), (0, 4) and (0, k) is 4 square units.
In ☐ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of ☐ABCD.

The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 20 cm | 40 cm | ? |
If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.

- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
