Question

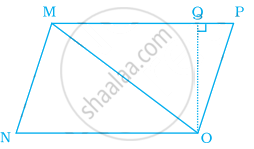
Ratio of areas of ∆MNO, ∆MOP and ∆MPQ in the given figure is ______.

विकल्प

• 2:1:3

• 1:3:2

• 2:3:1

• 1:2:3

Answer 1

Ratio of areas of ∆MNO, ∆MOP and ∆MPQ in the given figure is 2:1:3.

Explanation:

We know that, area of triangle = `1/2` × base × height

So, area of triangle MNO = `1/2` × NO × MO

= `1/2` × 5 × 4

= `1/2` × 20

= 10 cm²

Area of triangle MOP = `1/2` × MO × OP

= `1/2` × 5 × 2

= `1/2` × 10

= 5 cm²

Area of triangle MPQ = `1/2` × MO × PQ  ......[MP = MO]

= `1/2` × 5 × 6

= `1/2` × 30

= 15 cm²

So, the ratio of area = 10:5:15  ......[Divide each by 5]

Then we get, 2:1:3