Advertisements
Advertisements
Question
In the given figure, a rectangle with perimeter 264 cm is divided into five congruent rectangles. Find the perimeter of one of the rectangles.
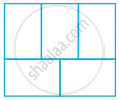
Solution
Let l and b the length and breadth of each rectangle, respectively.
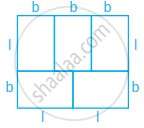
Given, perimeter of a rectangle = 264 cm
According to the figure, 4l + 5b = 264 ......(i)
and 2l = 3b ......(ii)
Put the value of 3b from equation (ii) in equation (i), 2(2l) + 5b = 264
⇒ 2 × 3b + 5b = 264
⇒ 6b + 5b = 264
⇒ 11b = 264
⇒ b = `264/11`
⇒ b = 24 cm
∴ l = `(3b)/2 = (3 xx 24)/2` = 36 cm
Hence, perimeter of the rectangle = 2(1 + b) = 2(36 + 24) = 120 cm.
APPEARS IN
RELATED QUESTIONS
The perimeter of a rectangle is 46 m and its length is 15 m. Find its :
(i) breadth
(ii) area
(iii) diagonal.
Each side of a rectangle is doubled. Find the ratio between :
(i) perimeters of the original rectangle and the resulting rectangle.
(ii) areas of the original rectangle and the resulting rectangle.
Find the perimeter of a rectangle whose:
length = 3.6 m and breadth = 2.4 m
A rectangular field has length = 160m and breadth = 120 m. Find:
(i) the perimeter of the field.
(ii) the length of fence required to enclose the field.
(iii) the cost of fencing the field at the rate of? 80 per meter.
A rectangular piece of paper has area = 24 cm² and length = 5 cm. Find its perimeter.
Sanju completes 12 rounds around a square park every day. If one side of the park is 120 m, find out in kilometres and metres the distance that Sanju covers daily.
Length of a rectangle is three times its breadth. Perimeter of the rectangle is 40 cm. Find its length and width.
A rectangular path of 60 m length and 3 m width is covered by square tiles of side 25 cm. How many tiles will there be in one row along its width? How many such rows will be there? Find the number of tiles used to make this path?
What is the radius of the largest circle that can be cut out of the rectangle measuring 10 cm in length and 8 cm in breadth?
In the given figure, perimeter of (ii) is greater than that of (i), but its area is smaller than that of (i).
 |
 |
| (i) | (ii) |
