Advertisements
Advertisements
Question
What is the radius of the largest circle that can be cut out of the rectangle measuring 10 cm in length and 8 cm in breadth?
Options
4 cm
5 cm
8 cm
10 cm
Solution
4 cm
Explanation:
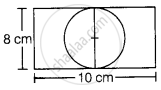
From the above figure, it is clear that largest circle will have diameter equal smaller side i.e. 8 cm
So, diameter = 8 cm
∴ Radius = `"Daimeter"/2` = 4 cm
APPEARS IN
RELATED QUESTIONS
A rectangular field is 30 m in length and 22m in width. Two mutually perpendicular roads, each 2.5 m wide, are drawn inside the field so that one road is parallel to the length of the field and the other road is parallel to its width. Calculate the area of the crossroads.
Find the perimeter of a rectangle whose:
length = 3.6 m and breadth = 2.4 m
Each side of a square field is 70 cm. How much distance will a boy walk in order to make?
(i) one complete round of this field?
(ii) 8 complete rounds of this field?
A school playground is rectangular in shape with length = 120 m and breadth = 90 m. Some school boys run along the boundary of the play-ground and make 15 complete rounds in 45 minutes. How much distance they run during this period.
If A denotes area of a rectangle, l represents its length and b represents its breadth, find:
l, if A = 48 cm² and b = 6 cm
Sanju completes 12 rounds around a square park every day. If one side of the park is 120 m, find out in kilometres and metres the distance that Sanju covers daily.
The length of a rectangular plot of land is 50 m and its width is 30 m. A triple fence has to be put along its edges. If the wire costs 60 rupees per metre, what will be the total cost of the wire needed for the fence?
Rahim and Peter go for a morning walk, Rahim walks around a square path of side 50 m and Peter walks around a rectangular path with length 40 m and breadth 30 m. If both of them walk 2 rounds each, who covers more distance and by how much?
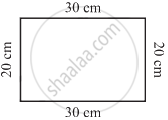
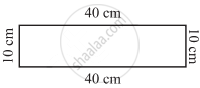
What is the perimeter of the following figures? What do you infer from the answers?
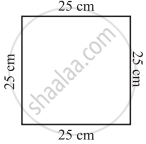 (a) |
 (c) |
 (b) |
 (d) |
In the given figure, perimeter of (ii) is greater than that of (i), but its area is smaller than that of (i).
 |
 |
| (i) | (ii) |
