Advertisements
Advertisements
Question
Using determinants, find the area of ΔPQR with vertices P(3, 1), Q(9, 3) and R(5, 7). Also, find the equation of line PQ using determinants.
Solution
Given vertices of triangle ΔPQR are P(3, 1), Q(9, 3) and R(5, 7).
Area of ΔPQR = `1/2 |(3, 1, 1),(9, 3, 1),(5, 7, 1)|`
= `1/2 {3(3 - 7) - (9 - 5) + (63 - 15)}`
= `1/2 {-12 - 4 + 48}`
= `1/2 xx 32`
= 16 sq. units.
APPEARS IN
RELATED QUESTIONS
Find the values of k so that the area of the triangle with vertices (k + 1, 1), (4, -3) and (7, -k) is 6 sq. units.
Find the area of the triangle PQR with Q(3,2) and the mid-points of the sides through Q being (2,−1) and (1,2).
Find the area of a triangle whose vertices are A(3, 2), B (11, 8) and C(8, 12).
For what value of k are the points (k, 2 – 2k), (–k + 1, 2k) and (–4 – k, 6 – 2k) are collinear ?
median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, - 6), B (3, - 2) and C (5, 2).
The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the following figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of Δ PQR if C is the origin?
Also calculate the areas of the triangles in these cases. What do you observe?
Find the area of a triangle with vertices at the point given in the following:
(1, 0), (6, 0), (4, 3)
Find values of k if area of triangle is 4 square units and vertices are (k, 0), (4, 0), (0, 2)
Find the area of the following triangle:

Find the area of the following triangle:

For what value of a point (a, 1), (1, -1) and (11, 4) are collinear?
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
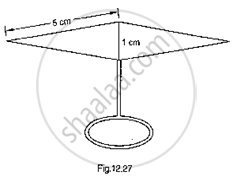
Find the area of the blades of thc magnetic compass shown in Fig.. 12.27. (Take √11 = 3.32).
Show that the points are the vertices of an isosceles right triangle.
Show that the points A (3,1) , B (0,-2) , C(1,1) and D (4,4) are the vertices of parallelogram ABCD.
For what value of k(k>0) is the area of the triangle with vertices (-2, 5), (k, -4) and (2k+1, 10) equal to 53 square units?
Using determinants, find the values of k, if the area of triangle with vertices (–2, 0), (0, 4) and (0, k) is 4 square units.
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
Find the area of the following triangle:

If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
In a triangle ABC, if `|(1, 1, 1),(1 + sin"A", 1 + sin"B", 1 + sin"C"),(sin"A" + sin^2"A", sin"B" + sin^2"B", sin"C" + sin^2"C")|` = 0, then prove that ∆ABC is an isoceles triangle.
Points A(3, 1), B(12, –2) and C(0, 2) cannot be the vertices of a triangle.
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 15 cm | 154.5 cm2 |
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 8.4 cm | 48.72 cm2 |
Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to ______.
Find the missing value:
| Base | Height | Area of Triangle |
| ______ | 31.4 mm | 1256 mm2 |
