Advertisements
Advertisements
Question
In a triangle ABC, if `|(1, 1, 1),(1 + sin"A", 1 + sin"B", 1 + sin"C"),(sin"A" + sin^2"A", sin"B" + sin^2"B", sin"C" + sin^2"C")|` = 0, then prove that ∆ABC is an isoceles triangle.
Solution
Let ∆ = `|(1, 1, 1),(1 + sin"A", 1 + sin"B", 1 + sin"C"),(sin"A" + sin^2"A", sin"B" + sin^2"B", sin"C" + sin^2"C")|`
= `|(1, 1, 1),(1 + sin"A", 1 + sin"B", 1 + sin"C"),(-cos^2"A", -cos^2"B", -cos^2"C")|` R3 → R3 – R2
= `|(1, 0, 0),(1 + sin"A", sin"B" - sin"A", sin"C" - sin"B"),(-cos^2"A", cos^2"A" - cos^2"B", cos^2"B" - cos^2"C")|` .......(C3 → C3 – C2 and C2 → C2 – C1)
Expanding along R1, we get
∆ = (sinB – sinA)(sin2C – sin2B) – (sinC – sin B)(sin2B – sin2A)
= (sinB – sinA)(sinC – sinB)(sinC – sin A)
= 0
⇒ Either sinB – sinA = 0 or sinC – sinB or sinC – sinA = 0
⇒ A = B or B = C or C = A
i.e. triangle ABC is isoceles.
APPEARS IN
RELATED QUESTIONS
Find the relation between x and y if, the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
Find the values of k for which the points A(k + 1, 2k), B(3k, 2k + 3) and (5k – 1, 5k) are collinear.
Find the values of k so that the area of the triangle with vertices (1, -1), (-4, 2k) and (-k, -5) is 24 sq. units.
Find the area of the quadrilateral ABCD whose vertices are respectively A(1, 1), B(7, –3), C(12, 2) and D(7, 21).
For what value of x will the points (x, –1), (2, 1) and (4, 5) lie on a line ?
Find the area of the triangle whose vertices are: (–5, –1), (3, –5), (5, 2)
median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, - 6), B (3, - 2) and C (5, 2).
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).
The vertices of a ΔABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that `(AD)/(AB) = (AE)/(AC) = 1/4`Calculate the area of the ΔADE and compare it with the area of ΔABC. (Recall Converse of basic proportionality theorem and Theorem 6.6 related to ratio of areas of two similar triangles)
Prove that the points (a, b), (a1, b1) and (a −a1, b −b1) are collinear if ab1 = a1b.
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm ?
In a ΔABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ΔABC and hence its altitude on AC ?
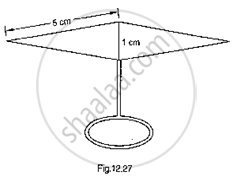
Find the area of the blades of thc magnetic compass shown in Fig.. 12.27. (Take √11 = 3.32).
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
Find the area of ΔABC with A(1, -4) and midpoints of sides through A being (2, -1) and (0, -1).
For what values of k are the points A(8, 1) B(3, -2k) and C(k, -5) collinear.
Prove that the points A (a,0), B( 0,b) and C (1,1) are collinear, if `( 1/a+1/b) =1`.
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
Find the area of the following triangle:

In ∆PQR, PR = 8 cm, QR = 4 cm and PL = 5 cm. 
Find:
(i) the area of the ∆PQR
(ii) QM.
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
If the points (3, -2), (x, 2), (8, 8) are collinear, then find the value of x.
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
Area of triangle MNO in the figure is ______.
Area of triangle PQR is 100 cm2 as shown in the below figure. If altitude QT is 10 cm, then its base PR is ______.

Find the missing value:
| Base | Height | Area of Triangle |
| ______ | 31.4 mm | 1256 mm2 |
