Advertisements
Advertisements
Question
Find the values of k for which the points A(k + 1, 2k), B(3k, 2k + 3) and (5k – 1, 5k) are collinear.
Solution
A(k + 1, 2k) , B(3k, 2k + 3) and (5k – 1, 5k)
If 3 points are collinear then area of triangle formed by them = 0
`1/2[(k+1)(2k+3-5k)- 2k(3k-5k+1)+1(15k^2- 10k^2- 2k+ 15k - 3)= 0`
`1/2[-3k^2+3k-3k+3+4k^2-2k+15k^2-10k^2-2k+15k-3]=0`
`1/2[6k^2+11k]=0`
`6k^2+11k=0`
`k=0,-11/6`
APPEARS IN
RELATED QUESTIONS
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).
For what value of k(k>0) is the area of the triangle with vertices (-2, 5), (k, -4) and (2k+1, 10) equal to 53 square units?
Find a relation between x and y, if the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 ?
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
Find the area of the following triangle:

Show that the ∆ABC is an isosceles triangle if the determinant
Δ = `[(1, 1, 1),(1 + cos"A", 1 + cos"B", 1 + cos"C"),(cos^2"A" + cos"A", cos^2"B" + cos"B", cos^2"C" + cos"C")]` = 0
The area of ∆ABC is 8 cm2 in which AB = AC = 4 cm and ∠A = 90º.
Find the area of the trapezium PQRS with height PQ given in the following figure.
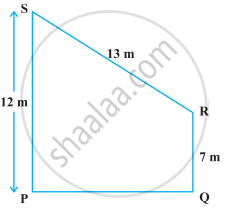
The area of a trapezium is 475 cm2 and the height is 19 cm. Find the lengths of its two parallel sides if one side is 4 cm greater than the other.
