Advertisements
Advertisements
प्रश्न
Using determinants, find the area of ΔPQR with vertices P(3, 1), Q(9, 3) and R(5, 7). Also, find the equation of line PQ using determinants.
उत्तर
Given vertices of triangle ΔPQR are P(3, 1), Q(9, 3) and R(5, 7).
Area of ΔPQR = `1/2 |(3, 1, 1),(9, 3, 1),(5, 7, 1)|`
= `1/2 {3(3 - 7) - (9 - 5) + (63 - 15)}`
= `1/2 {-12 - 4 + 48}`
= `1/2 xx 32`
= 16 sq. units.
APPEARS IN
संबंधित प्रश्न
Find the area of the triangle ABC with A(1, −4) and mid-points of sides through A being (2, −1) and (0, −1).
If the points A(−1, −4), B(b, c) and C(5, −1) are collinear and 2b + c = 4, find the values of b and c.
If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the coordniates of any point P, if PA = PB and Area of ∆PAB = 10
Find the area of the triangle whose vertices are: (2, 3), (-1, 0), (2, -4)
The vertices of a ΔABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that `(AD)/(AB) = (AE)/(AC) = 1/4`Calculate the area of the ΔADE and compare it with the area of ΔABC. (Recall Converse of basic proportionality theorem and Theorem 6.6 related to ratio of areas of two similar triangles)
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm ?
If G(-2, 1) is the centroid of a ΔABC and two of its vertices are A(1, -6) and B(-5, 2) , find the third vertex of the triangle.
Find the third vertex of a ΔABC if two of its vertices are B(-3,1) and C (0,-2) and its centroid is at the origin
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
For what value of x are the points A(-3, 12), B(7, 6) and C(x, 9) collinear.
Find the value(s) of p for which the points (3p + 1, p), (p + 2, p – 5) and (p + 1, –p) are collinear ?
If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 ?
Find the value(s) of k so that the quadratic equation x2 − 4kx + k = 0 has equal roots.

In Figure 1, PS = 3 cm, QS = 4 cm, ∠PRQ = θ, ∠PSQ = 90°, PQ ⊥ RQ and RQ = 9 cm. Evaluate tan θ.
What is the area of a triangle with base 4.8 cm and height 3.6 cm?
A(6, 1), B(8, 2) and C(9, 4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ∆ADE.
If the points A(1, 2), O(0, 0) and C(a, b) are collinear, then ______.
Find the coordinates of the point Q on the x-axis which lies on the perpendicular bisector of the line segment joining the points A(–5, –2) and B(4, –2). Name the type of triangle formed by the points Q, A and B.
Find the area of the triangle whose vertices are (–8, 4), (–6, 6) and (–3, 9).
If `D((-1)/2, 5/2), E(7, 3)` and `F(7/2, 7/2)` are the midpoints of sides of ∆ABC, find the area of the ∆ABC.
The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
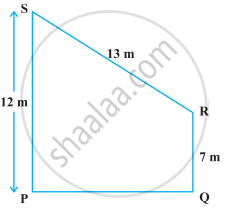
Find the area of the trapezium PQRS with height PQ given in the following figure.
The area of a triangle with vertices A, B, C is given by ______.
Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
Ratio of the area of ∆WXY to the area of ∆WZY is 3:4 in the given figure. If the area of ∆WXZ is 56 cm2 and WY = 8 cm, find the lengths of XY and YZ.

In the given figure, area of ΔPQR is 20 cm2 and area of ΔPQS is 44 cm2. Find the length RS, if PQ is perpendicular to QS and QR is 5 cm.

