Advertisements
Advertisements
Question
Find the value of y for which the points A(-3, 9), B(2,y) and C(4,-5) are collinear.
Solution
Let `A(x_1=-3,y_1=9),B(x_2=2,y_2=y) and C(x_3=4, y_3=-5)` be the given points
The given points are collinear if
`x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_2-y_2)=0`
`⇒(-3)(y+5)+2(-5-9)+4(9-y)=0`
`⇒ -3y-15-28+36-4y=0`
⇒7y = 36-43
⇒y = -1
APPEARS IN
RELATED QUESTIONS
For what value of x will the points (x, –1), (2, 1) and (4, 5) lie on a line ?
Find equation of line joining (3, 1) and (9, 3) using determinant.
Find the missing value:
| Base | Height | Area of triangle |
| 15 cm | ______ | 87 cm2 |
If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA2+ PB2 + PC2 = GA2 + GB2 + GC2 + 3GP2.
In ☐ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of ☐ABCD.

The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
The area of a trapezium is 475 cm2 and the height is 19 cm. Find the lengths of its two parallel sides if one side is 4 cm greater than the other.
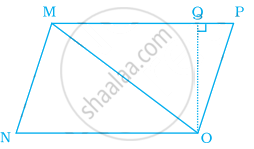
Area of triangle MNO in the figure is ______.
In the given figure, if PR = 12 cm, QR = 6 cm and PL = 8 cm, then QM is ______.

Find the missing value:
| Base | Height | Area of Triangle |
| ______ | 31.4 mm | 1256 mm2 |
