Advertisements
Advertisements
Question
Prove that the points A(2, 4), b(2, 6) and (2 +
Solution
The given points are A(2, 4), b(2, 6) and (2 +
Hence, the points A(2, 4), b(2, 6) and (2 +
APPEARS IN
RELATED QUESTIONS
Prove that the area of a triangle with vertices (t, t −2), (t + 2, t + 2) and (t + 3, t) is independent of t.
Find the area of the triangle PQR with Q(3,2) and the mid-points of the sides through Q being (2,−1) and (1,2).
Find the centre of a circle passing through the points (6, − 6), (3, − 7) and (3, 3).
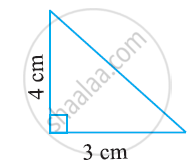
Find the area of the following triangle:
Find the area of the quadrilaterals, the coordinates of whose vertices are
(1, 2), (6, 2), (5, 3) and (3, 4)
The point A divides the join of P (−5, 1) and Q(3, 5) in the ratio k:1. Find the two values of k for which the area of ΔABC where B is (1, 5) and C(7, −2) is equal to 2 units.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm ?
Find the value of k so that the area of the triangle with vertices A (k+1, 1), B(4, -3) and C(7, -k) is 6 square units
Find the value of m if the points (5, 1), (–2, –3) and (8, 2m) are collinear.
If area of a triangular piece of cardboard is 90 cm2, then the length of altitude corresponding to 20 cm long base is ______ cm.
