Advertisements
Advertisements
प्रश्न
A rhombus shaped sheet with perimeter 40 cm and one diagonal 12 cm, is painted on both sides at the rate of Rs 5 per m2. Find the cost of painting.
उत्तर
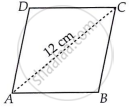
Let ABCD be a rhombus having sides AB = BC = CD = DA = x cm
Given that perimeter of a rhombus = 40 cm
`\implies` x + x + x + x = 40
`\implies` 4x = 40
`\implies x = 40/4`
∴ x = 10
In ΔABC, let a = AB = 10 cm, b = BC = 10 cm and c = AC = 12 cm
Now, semi-perimeter of a ΔABC,
`s = (a + b + c)/2`
= `((10 + 10 + 12)/2) cm`
= `32/2 cm`
= 16 cm
∴ Area of ΔABC = `sqrt(s(s - a)(s - b)(s - c))`
= `sqrt(16(16 - 10)(16 - 10)(16 - 12)) cm^2`
= `sqrt(16 xx 6 xx 6 xx 4) cm^2`
= 48 cm2
Now, area of the rhombus ABCD
= 2(Area of ΔABC)
= (2 × 48) cm2
= 96 cm2
∵ Cost of painting the sheet of 1 cm2 = Rs. 5
∴ Cost of painting the sheet of 96 cm2
= Rs. (96 × 5)
= Rs. 480
Thus, the cost of painting the sheet on both sides = Rs. (2 × 480) = Rs. 960
APPEARS IN
संबंधित प्रश्न
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
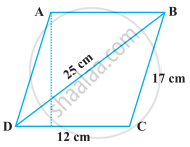
Some measures are given in the adjacent figure, find the area of ☐ABCD.
Find the area of the triangle formed by the points
(–10, –4), (–8, –1) and (–3, –5)
The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (3, −2). The third vertex is (x, y) where y = x + 3. Find the coordinates of the third vertex.
Using Heron’s formula, find the area of a triangle whose sides are 10 cm, 24 cm, 26 cm
The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
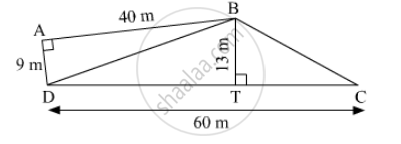
Find the area of a parallelogram given in figure. Also find the length of the altitude from vertex A on the side DC.
The perimeter of a triangular field is 420 m and its sides are in the ratio 6 : 7 : 8. Find the area of the triangular field.
A field is in the shape of a trapezium having parallel sides 90 m and 30 m. These sides meet the third side at right angles. The length of the fourth side is 100 m. If it costs Rs 4 to plough 1 m2 of the field, find the total cost of ploughing the field.
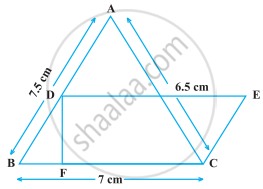
In the following figure, ∆ABC has sides AB = 7.5 cm, AC = 6.5 cm and BC = 7 cm. On base BC a parallelogram DBCE of same area as that of ∆ABC is constructed. Find the height DF of the parallelogram.