Advertisements
Online Mock Tests
Chapters
2: Polynomials
3: Coordinate Geometry
4: Linear Equation In Two Variables
5: Introduction To Euclid's Geometry
6: Lines & Angles
7: Triangles
8: Quadrilaterals
9: Areas of Parallelograms & Triangles
10: Circles
11: Construction
▶ 12: Heron's Formula
13: Surface Area & Volumes
14: Statistics & Probability
![NCERT Exemplar solutions for Mathematics [English] Class 9 chapter 12 - Heron's Formula NCERT Exemplar solutions for Mathematics [English] Class 9 chapter 12 - Heron's Formula - Shaalaa.com](/images/mathematics-english-class-9_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 12: Heron's Formula
Below listed, you can find solutions for Chapter 12 of CBSE NCERT Exemplar for Mathematics [English] Class 9.
NCERT Exemplar solutions for Mathematics [English] Class 9 12 Heron's Formula Exercise 12.1 [Pages 113 - 114]
State whether the following statement is True or False:
An isosceles right triangle has area 8 cm2. The length of its hypotenuse is ______.
`sqrt(32)` cm
`sqrt(16)` cm
`sqrt(48)` cm
`sqrt(24)` cm
The perimeter of an equilateral triangle is 60 m. The area is ______.
`10sqrt(3)` m2
`15sqrt(3)` m2
`20sqrt(3)` m2
`100sqrt(3)` m2
The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is ______.
1322 cm2
1311 cm2
1344 cm2
1392 cm2
The area of an equilateral triangle with side `2sqrt(3)` cm is ______.
5.196 cm2
0.866 cm2
3.496 cm2
1.732 cm2
The length of each side of an equilateral triangle having an area of `9sqrt(3)`cm2 is ______.
8 cm
36 cm
4 cm
6 cm
If the area of an equilateral triangle is `16sqrt(3)` cm2, then the perimeter of the triangle is ______.
48 cm
24 cm
12 cm
36 cm
The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude ______.
`16sqrt(5)` cm
`10sqrt(5)` cm
`24sqrt(5)` cm
28 cm
The area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm, is ______.
`sqrt(15)` cm2
`sqrt(15/2)` cm2
`2sqrt(15)` cm2
`4sqrt(15)` cm2
The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is ______.
Rs 2.00
Rs 2.16
Rs 2.48
Rs 3.00
NCERT Exemplar solutions for Mathematics [English] Class 9 12 Heron's Formula Exercise 12.2 [Page 115]
State whether the following statement is True or False:
The area of a triangle with base 4 cm and height 6 cm is 24 cm2.
True
False
The area of ∆ABC is 8 cm2 in which AB = AC = 4 cm and ∠A = 90º.
True
False
The area of the isosceles triangle is `5/4 sqrt(11)` cm2, if the perimeter is 11 cm and the base is 5 cm.
True
False
The area of the equilateral triangle is `20sqrt(3)` cm2 whose each side is 8 cm.
True
False
If the side of a rhombus is 10 cm and one diagonal is 16 cm, the area of the rhombus is 96 cm2.
True
False
The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
True
False
The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
True
False
The cost of levelling the ground in the form of a triangle having the sides 51 m, 37 m and 20 m at the rate of Rs 3 per m2 is Rs 918.
True
False
In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
True
False
NCERT Exemplar solutions for Mathematics [English] Class 9 12 Heron's Formula Exercise 12.3 [Page 117]
Find the cost of laying grass in a triangular field of sides 50 m, 65 m and 65 m at the rate of Rs 7 per m2.
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 13 m, 14 m and 15 m. The advertisements yield an earning of Rs 2000 per m2 a year. A company hired one of its walls for 6 months. How much rent did it pay?
From a point in the interior of an equilateral triangle, perpendiculars are drawn on the three sides. The lengths of the perpendiculars are 14 cm, 10 cm and 6 cm. Find the area of the triangle.
The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3 : 2. Find the area of the triangle.
Find the area of a parallelogram given in figure. Also find the length of the altitude from vertex A on the side DC.
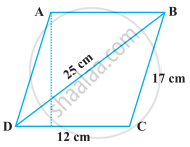
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
The perimeter of a triangular field is 420 m and its sides are in the ratio 6 : 7 : 8. Find the area of the triangular field.
The sides of a quadrilateral ABCD are 6 cm, 8 cm, 12 cm and 14 cm (taken in order) respectively, and the angle between the first two sides is a right angle. Find its area.
A rhombus shaped sheet with perimeter 40 cm and one diagonal 12 cm, is painted on both sides at the rate of Rs 5 per m2. Find the cost of painting.
Find the area of the trapezium PQRS with height PQ given in the following figure.
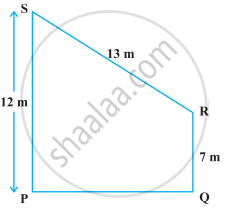
NCERT Exemplar solutions for Mathematics [English] Class 9 12 Heron's Formula Exercise 12.4 [Pages 118 - 120]
How much paper of each shade is needed to make a kite given in the following figure, in which ABCD is a square with diagonal 44 cm.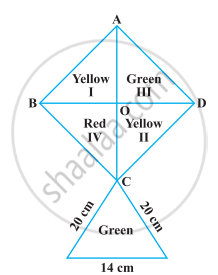
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
The area of a trapezium is 475 cm2 and the height is 19 cm. Find the lengths of its two parallel sides if one side is 4 cm greater than the other.
A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
A field is in the shape of a trapezium having parallel sides 90 m and 30 m. These sides meet the third side at right angles. The length of the fourth side is 100 m. If it costs Rs 4 to plough 1 m2 of the field, find the total cost of ploughing the field.
In the following figure, ∆ABC has sides AB = 7.5 cm, AC = 6.5 cm and BC = 7 cm. On base BC a parallelogram DBCE of same area as that of ∆ABC is constructed. Find the height DF of the parallelogram.
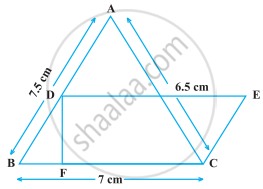
The dimensions of a rectangle ABCD are 51 cm × 25 cm. A trapezium PQCD with its parallel sides QC and PD in the ratio 9 : 8, is cut off from the rectangle as shown in the following figure. If the area of the trapezium PQCD is `5/6` th part of the area of the rectangle, find the lengths QC and PD.

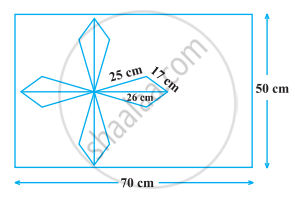
A design is made on a rectangular tile of dimensions 50 cm × 70 cm as shown in the following figure. The design shows 8 triangles, each of sides 26 cm, 17 cm and 25 cm. Find the total area of the design and the remaining area of the tile.
Solutions for 12: Heron's Formula
![NCERT Exemplar solutions for Mathematics [English] Class 9 chapter 12 - Heron's Formula NCERT Exemplar solutions for Mathematics [English] Class 9 chapter 12 - Heron's Formula - Shaalaa.com](/images/mathematics-english-class-9_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [English] Class 9 chapter 12 - Heron's Formula
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 9 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [English] Class 9 CBSE 12 (Heron's Formula) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 9 chapter 12 Heron's Formula are Area of a Triangle by Heron's Formula, Application of Heron’s Formula in Finding Areas of Quadrilaterals, Area of a Triangle.
Using NCERT Exemplar Mathematics [English] Class 9 solutions Heron's Formula exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 9 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 12, Heron's Formula Mathematics [English] Class 9 additional questions for Mathematics Mathematics [English] Class 9 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
