NCERT Exemplar solutions for Mathematics [English] Class 9 chapter 7 - Triangles [Latest edition]

Which of the following is not a criterion for congruence of triangles?

If AB = QR, BC = PR and CA = PQ, then ______.

In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.

In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to ______.

In ∆PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is ______.

D is a point on the side BC of a ∆ABC such that AD bisects ∠BAC. Then ______.

It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?

Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.

In ∆PQR, if ∠R > ∠Q, then ______.

In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.

In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.

In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side AB of ∆ABC so that the two triangles are congruent? Give reason for your answer.

In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side BC of ∆ABC so that the two triangles are congruent? Give reason for your answer.

“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?

“If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?

Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.

It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?

If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer

In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.

AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.

M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM? Give reason for your answer.

Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.

Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.

ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.

In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.

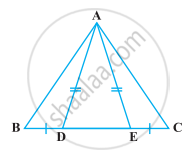
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.

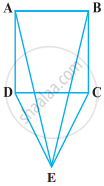
In the following figure, BA ⊥ AC, DE ⊥ DF such that BA = DE and BF = EC. Show that ∆ABC ≅ ∆DEF.

Q is a point on the side SR of a ∆PSR such that PQ = PR. Prove that PS > PQ.

S is any point on side QR of a ∆PQR. Show that: PQ + QR + RP > 2PS.

D is any point on side AC of a ∆ABC with AB = AC. Show that CD < BD.

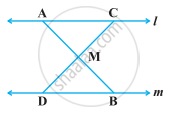
In the following figure, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.

Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.

Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC

In the following figure, AD is the bisector of ∠BAC. Prove that AB > BD.

Find all the angles of an equilateral triangle.

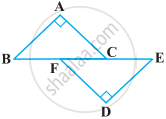
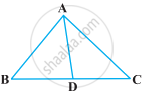
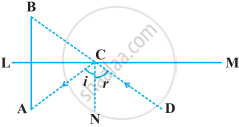
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.

[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].

ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:

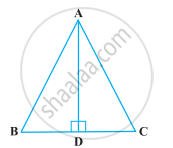
In ∆ABD and ∆ACD,

AB = AC (Given)

∠B = ∠C (Because AB = AC)

and ∠ADB = ∠ADC

Therefore, ∆ABD ≅ ∆ACD (AAS)

So, ∠BAD = ∠CAD (CPCT)

What is the defect in the above arguments?

[Hint: Recall how ∠B = ∠C is proved when AB = AC].

P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.

ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.

ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.

O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.

ABC and DBC are two triangles on the same base BC such that A and D lie on the opposite sides of BC, AB = AC and DB = DC. Show that AD is the perpendicular bisector of BC.

ABC is an isosceles triangle in which AC = BC. AD and BE are respectively two altitudes to sides BC and AC. Prove that AE = BD.

Prove that sum of any two sides of a triangle is greater than twice the median with respect to the third side.

Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)

Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD

In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.

In a right triangle, prove that the line-segment joining the mid-point of the hypotenuse to the opposite vertex is half the hypotenuse.

Two lines l and m intersect at the point O and P is a point on a line n passing through the point O such that P is equidistant from l and m. Prove that n is the bisector of the angle formed by l and m.

Line segment joining the mid-points M and N of parallel sides AB and DC, respectively of a trapezium ABCD is perpendicular to both the sides AB and DC. Prove that AD = BC.

ABCD is a quadrilateral such that diagonal AC bisects the angles A and C. Prove that AB = AD and CB = CD.

ABC is a right triangle such that AB = AC and bisector of angle C intersects the side AB at D. Prove that AC + AD = BC.

AB and CD are the smallest and largest sides of a quadrilateral ABCD. Out of ∠B and ∠D decide which is greater.

Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than `2/3` of a right angle.

ABCD is quadrilateral such that AB = AD and CB = CD. Prove that AC is the perpendicular bisector of BD.