Advertisements
Advertisements
प्रश्न
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
उत्तर
No, it is not possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm because here we see that sum of the lengths of two sides is equal to third side i.e., 4 + 3 = 7.
As we know that, the sum of any two sides of a triangle is greater than its third side, so given statement is not correct.
APPEARS IN
संबंधित प्रश्न
In the given figure, if AE || DC and AB = AC, the value of ∠ABD is
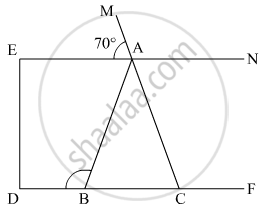
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
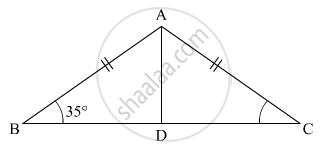
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
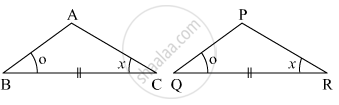
From the information shown in the figure,
In ΔABC and ΔPQR
∠ABC ≅ ∠PQR
seg BC ≅ seg QR
∠ACB ≅ ∠PRQ
∴ ΔABC ≅ ΔPQR ...`square` test
∴ ∠BAC ≅ `square` ...corresponding angles of congruent triangles.
`{:("seg AB" ≅ square),("and" square ≅ "seg PR"):}}` ...corresponding sides of congruent triangles
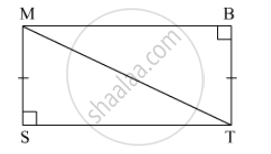
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
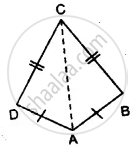
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.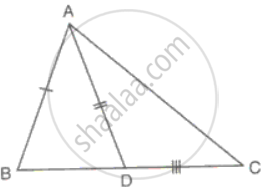
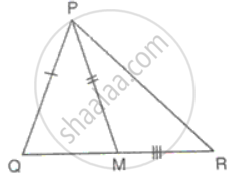
In ΔABC, AD is a median. The perpendiculars from B and C meet the line AD produced at X and Y. Prove that BX = CY.
Given that ∆ABC ≅ ∆DEF List all the corresponding congruent sides
Which of the following rule is not sufficient to verify the congruency of two triangles
