Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
Notes
Congruence of Triangles:
Two triangles are congruent if the sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle.
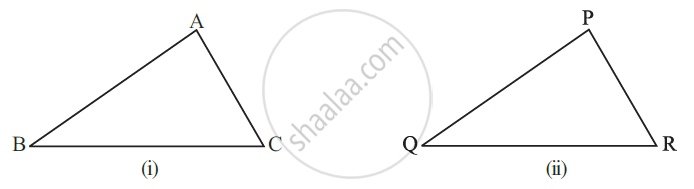
△ ABC and △ PQR have the same size and shape. They are congruent.
△ABC ≅ △PQR
This means that, when you place △PQR on △ABC, P falls on A, Q falls on B and R falls on C, also PQ falls along `bar"AB", bar"QR" "falls along" bar"BC" and bar"PR" "falls along" bar"AC"`.
If, under a given correspondence, two triangles are congruent, then their corresponding parts (i.e., angles and sides) that match one another are equal.
Thus, in these two congruent triangles.
We have:
-
Corresponding vertices: A and P, B and Q, C, and R.
-
Corresponding sides: `bar"AB" and bar"PQ", bar"BC" and bar"QR", bar"AC" and bar"PR"`.
-
Corresponding angles: ∠A and ∠P, ∠B and ∠Q, ∠C, and ∠R.
Congruent triangles corresponding parts in short ‘CPCT’ stands for corresponding parts of congruent triangles.
Example
∆ABC and ∆PQR are congruent under the correspondence:
ABC ↔ RQP
Write the parts of ∆ABC that correspond to
(i) `bar"PQ"`
(ii)∠Q
(iii) `bar"RP"`
For a better understanding of the correspondence, let us use a diagram

The correspondence is ABC ↔ RQP.
This means A ↔ R; B ↔ Q; and C ↔ P.
So,
(i) `bar"PQ" ↔ bar"CB"`
(ii) ∠Q ↔ ∠B and
(iii) `bar"RP" ↔ bar"AC"`.