Advertisements
Advertisements
प्रश्न
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
उत्तर
Given:
ABCD is a parallelogram, where BE = CE
To prove:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
a. In ΔDCE and ΔLBE
∠DCE = ∠EBL ....[DC || AB, alternate angles]
CE = BE ....[given]
∠DEC = ∠LEB ....[vertically opposite angles]
∴ By Angle-Side-Angle criterion of congruence,
ΔDCE ≅ ΔLBE
The corresponding parts of the congruent triangles are congruent.
∴ DC = LB ....(1)
b. DC = AB ....(2)[opposite sides of a parallelogram]
From (1) and (2),
AB = BL ....(3)
c. Al = AB + BL
⇒ AL = Ab + AB ....[From (3)]
⇒ AL = 2AB
⇒ Al = 2DC. ....[From (2)]
APPEARS IN
संबंधित प्रश्न
ΔPQR and ΔABC is not congruent to ΔRPQ, then which of the following is not true:
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
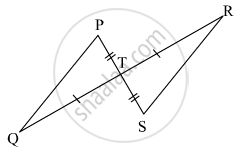
From the information shown in the figure,
in ΔPTQ and ΔSTR
seg PT ≅ seg ST
∠PTQ ≅ ∠STR ...[Vertically opposite angles]
∴ ΔPTQ ≅ ΔSTR ...`square` test
∴ `{:("∠TPQ" ≅ square),("and" square ≅ "∠TRS"):}}` ...corresponding angles of congruent triangles
seg PQ ≅ `square` ...corresponding sides of congruent triangles
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

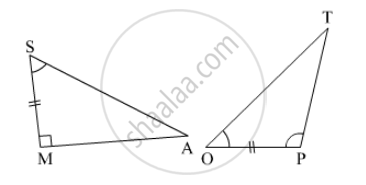
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(BC = 5cm,AC = 6cm,∠C = 80°);
ΔXYZ;(XZ = 6cm,XY = 5cm,∠X = 70°).
PQRS is a quadrilateral and T and U are points on PS and RS respectively such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles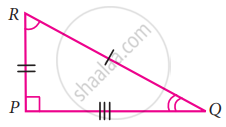

In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.
ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
