Advertisements
Advertisements
प्रश्न
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

उत्तर
The triangle is congruent by Hypotenuse side test, in the correspondence KJI ↔ LJI.
संबंधित प्रश्न
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
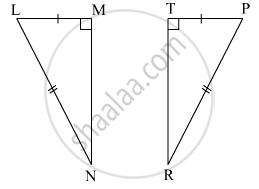
By ______ test
ΔLMN ≅ ΔPTR
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
State, whether the pairs of triangles given in the following figures are congruent or not:
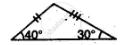
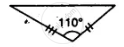
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.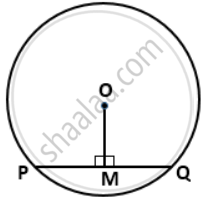
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.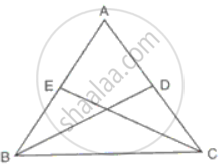
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
