Advertisements
Advertisements
प्रश्न
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.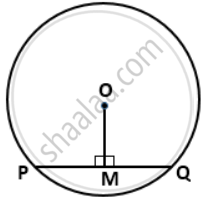
उत्तर
Given:
In the figure, O is centre of the circle and PQ is a chord.
OM ⊥ PQ
To prove: PM = QM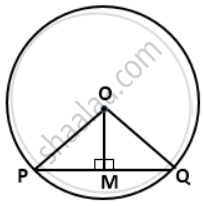
Construction: Join Op and OQ
Proof:
In right triangles ΔOPM and ΔOQM,
OP = OQ ....[radii of the same circle]
OM = OM ....[common]
∴ By right angle-Hypotenuse-Side criterion of congruency,
ΔOPM ≅ΔOQM
The corresponding parts of the congruent triangles are congruent.
∴ PM = QM.
APPEARS IN
संबंधित प्रश्न
In ΔPQR ≅ ΔEFD then ED =
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

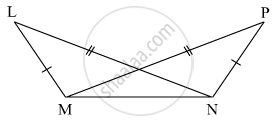
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
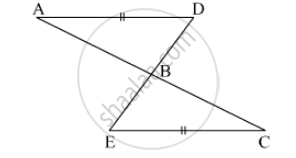
In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
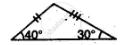
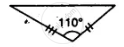
State, whether the pairs of triangles given in the following figures are congruent or not:
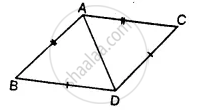
In the given figure, prove that: ∆ ABD ≅ ∆ ACD
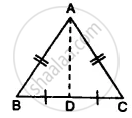
Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
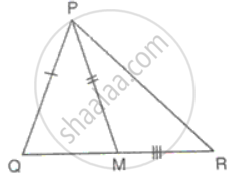
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.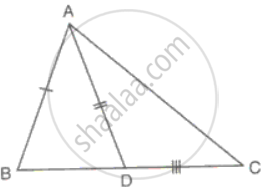
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles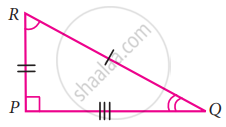

In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side AB of ∆ABC so that the two triangles are congruent? Give reason for your answer.
