Advertisements
Advertisements
प्रश्न
In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.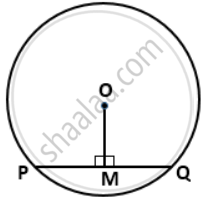
उत्तर
Given:
In the figure, O is centre of the circle and PQ is a chord.
OM ⊥ PQ
To prove: PM = QM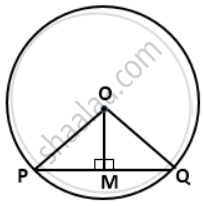
Construction: Join Op and OQ
Proof:
In right triangles ΔOPM and ΔOQM,
OP = OQ ....[radii of the same circle]
OM = OM ....[common]
∴ By right angle-Hypotenuse-Side criterion of congruency,
ΔOPM ≅ΔOQM
The corresponding parts of the congruent triangles are congruent.
∴ PM = QM.
APPEARS IN
संबंधित प्रश्न
If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the Corresponding congruent parts of the triangles.
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
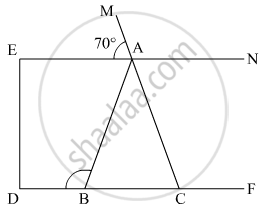
In the given figure, if AE || DC and AB = AC, the value of ∠ABD is
In the following example, a pair of triangles is shown. Equal parts of triangles in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
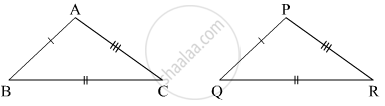
By ______ test
Δ ABC ≅ ΔPQR
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
State, whether the pairs of triangles given in the following figures are congruent or not:
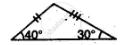
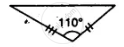
In the given figure, prove that: ∆ ABD ≅ ∆ ACD
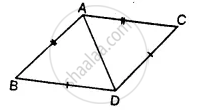
In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
In the figure, ∠BCD = ∠ADC and ∠ACB =∠BDA. Prove that AD = BC and ∠A = ∠B.
