Advertisements
Advertisements
प्रश्न
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
उत्तर
Given: ABCD is a Square and ΔAPB is an equilateral triangle.
We need to
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC
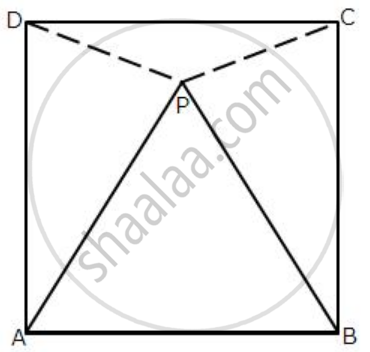
Proof:
Since AB side is present in both square & equilateral triangle
AP = PB = AB =AD = CD = BC
(i) In ΔBPC,
BP = BC
∴ ∠BPC = ∠PCB
∠BPC + ∠PCB + 30° = 180°
∠BPC + ∠BPC = 150°
2∠BPC = ` (150°)/2 = 75°`
∴ ∠BPC = ∠PCB = 75°
∠ADP = ∠DPA = 75° ...[C.P.C.T.C]
(ii) In DPC
∠DCP = 90° - 75° = 15°
∠PDC = 90° - 75° = 15°
∠DPC = 180° - (15° + 15°)
∠DPC = 150°
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠F
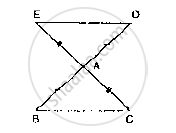
In Fig. 10.22, the sides BA and CA have been produced such that: BA = AD and CA = AE.
Prove that segment DE || BC.
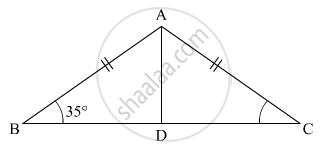
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
From the information shown in the figure,
In ΔABC and ΔPQR
∠ABC ≅ ∠PQR
seg BC ≅ seg QR
∠ACB ≅ ∠PRQ
∴ ΔABC ≅ ΔPQR ...`square` test
∴ ∠BAC ≅ `square` ...corresponding angles of congruent triangles.
`{:("seg AB" ≅ square),("and" square ≅ "seg PR"):}}` ...corresponding sides of congruent triangles
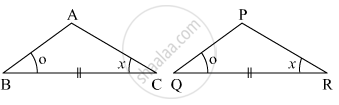
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
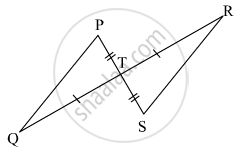
From the information shown in the figure,
in ΔPTQ and ΔSTR
seg PT ≅ seg ST
∠PTQ ≅ ∠STR ...[Vertically opposite angles]
∴ ΔPTQ ≅ ΔSTR ...`square` test
∴ `{:("∠TPQ" ≅ square),("and" square ≅ "∠TRS"):}}` ...corresponding angles of congruent triangles
seg PQ ≅ `square` ...corresponding sides of congruent triangles
On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
The congruent figures super impose each other completely.
