Advertisements
Advertisements
प्रश्न
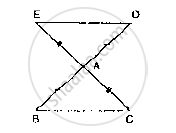
In Fig. 10.22, the sides BA and CA have been produced such that: BA = AD and CA = AE.
Prove that segment DE || BC.
उत्तर
Given that, the sides BA and CA have been produced such that BA =AD and CA= AE and
given to prove DE || BC
Consider triangle BAC and , DAE
We have
BA = ADand CA = AE [∵ given in the data]
And also ∠BAC=∠DAE [ ∵vertically opposite
angles]
So, by SAS congruence criterion, we have ΔBAC ≅ ΔDAE
⇒ BC = DE and ∠DEA=∠BCA, ∠EDA ∠CBA
[Corresponding parts of congruent triangles are equal]
Now, DE and BC are two lines intersected by a transversal DB such that ∠DEA =∠BCA,
i.e., alternate angles are equal
Therefore, DE || BC
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(DF)`
If ΔABC ≅ ΔABC is isosceles with
In triangles ABC and PQR three equality relations between some parts are as follows:
AB = QP, ∠B = ∠P and BC = PR
State which of the congruence conditions applies:
Which of the following is not a criterion for congruence of triangles?
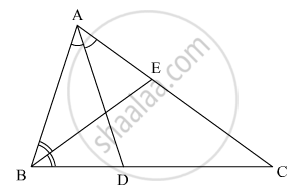
In the given figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that ADbisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
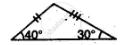
State, whether the pairs of triangles given in the following figures are congruent or not:
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
In the given figure, AB = DB and AC = DC. Find the values of x and y.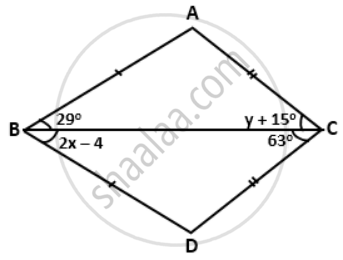
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side AB of ∆ABC so that the two triangles are congruent? Give reason for your answer.
