Advertisements
Advertisements
प्रश्न
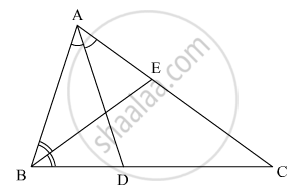
In the given figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that ADbisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
पर्याय
72°
73°
74°
95°
उत्तर
It is given that
∠B = 2∠C,
AB = CD
∠BAD = DAC
∠ABE = ∠EBC
We have to find ∠BAC

Now AB = CD
AB = BD
Now the triangle is isosceles
∠B = 2∠C
Let
∠B = x
∠B = 2x
∠C = x
So ∠B = ∠A
Now
∠A + ∠B + ∠C = 180°
2x + 2x + x = 180°
5x = 180°
x = 36°
Since
∠A = 2x
= `2 xx 36°
= 72°
APPEARS IN
संबंधित प्रश्न
In a ΔABC, if AB = AC and BC is produced to D such that ∠ACD = 100°, then ∠A =
In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
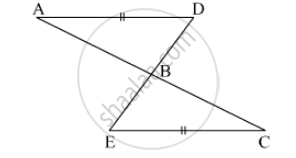
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: ΔAMC≅ ΔANB

State, whether the pairs of triangles given in the following figures are congruent or not:

Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 70°,BC = 6cm,∠C = 50°);
ΔXYZ;(∠Z = 60°,XY = 6cm,∠X = 70°).
In the figure, BM and DN are both perpendiculars on AC and BM = DN. Prove that AC bisects BD.
ΔABC is isosceles with AB = AC. BD and CE are two medians of the triangle. Prove that BD = CE.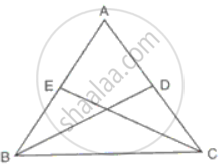
In ΔABC, AB = AC. D is a point in the interior of the triangle such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ΔABC.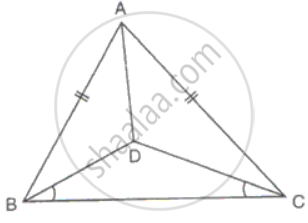
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
