Advertisements
Advertisements
Question
In the given figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that ADbisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
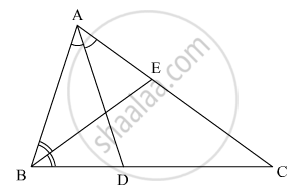
Options
72°
73°
74°
95°
Solution
It is given that
∠B = 2∠C,
AB = CD
∠BAD = DAC
∠ABE = ∠EBC
We have to find ∠BAC

Now AB = CD
AB = BD
Now the triangle is isosceles
∠B = 2∠C
Let
∠B = x
∠B = 2x
∠C = x
So ∠B = ∠A
Now
∠A + ∠B + ∠C = 180°
2x + 2x + x = 180°
5x = 180°
x = 36°
Since
∠A = 2x
= `2 xx 36°
= 72°
APPEARS IN
RELATED QUESTIONS
ΔPQR and ΔABC is not congruent to ΔRPQ, then which of the following is not true:
In the given figure, X is a point in the interior of square ABCD. AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then BY =

In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that:
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that: AD = CE.
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB
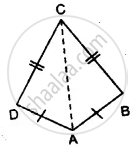
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
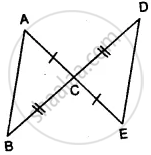
If the perpendicular bisector of the sides of a triangle PQR meet at I, then prove that the line joining from P, Q, R to I are equal.
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of ∆PQR should be equal to side BC of ∆ABC so that the two triangles are congruent? Give reason for your answer.
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
