Advertisements
Advertisements
Question
If the perpendicular bisector of the sides of a triangle PQR meet at I, then prove that the line joining from P, Q, R to I are equal.
Solution
Given:
In ΔPQR,
PA is the perpendicular bisector of QR ⇒ QA = RA
RC is the perpendicular bisector of PQ ⇒ PC = QC
QB is the perpendicular bisector of PR ⇒ PR = RB
PA, RC and QB meet at I.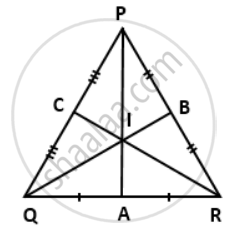
To prove: IP = IQ = IR
Proof:
In ΔQIA and ΔRIA
QA = RA ....[Given]
∠QAI = ∠RAI ....[Each = 90]
IA = IA ....[Common]
∴ By Side-Angle-Side criterion of congruence,
ΔIQ = IR ....(i)
Similarly, in ΔRIB and ΔPIB
RB = PB ...[Given]
∠RBI = ∠PBI ...[Each = 90°]
IB = IB ...[Common]
∴ By Side-Angle-Side criterion of congruence,
ΔRIB ≅ ΔPIB
The corresponding parts of the congruent triangles are congruent.
∴ IR = IP ....(ii)
From (i) and (ii), we have
IP = IQ = IR.
APPEARS IN
RELATED QUESTIONS
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangles in each pair are congruent.
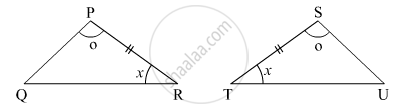
By ______ test
ΔPRQ ≅ ΔSTU
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
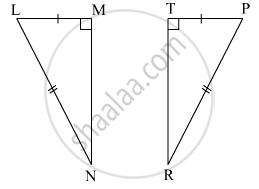
By ______ test
ΔLMN ≅ ΔPTR
In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that: AD = CE.
State, whether the pairs of triangles given in the following figures are congruent or not:
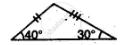
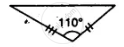
State, whether the pairs of triangles given in the following figures are congruent or not:
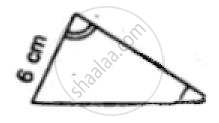

Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
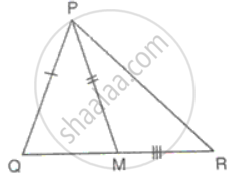
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.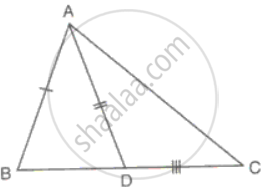
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR? Why?
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆ABC ≅ ∆LMN
