Advertisements
Advertisements
Question
State, whether the pairs of triangles given in the following figures are congruent or not:
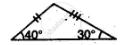
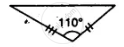
Solution
In the first A, third angle
= 180° – (40°+ 30°)
= 180° – 70°
= 110°
Now in these two triangles the sides and included angle of the one are equal to the corresponding sides and included angle.
Hence these are congruent triangles
(S.A.S. axiom)
APPEARS IN
RELATED QUESTIONS
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
Which of the following is not a criterion for congruence of triangles?
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
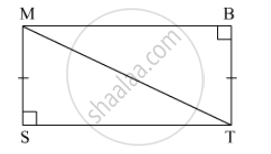
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that: AD = CE.
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 8cm,BC = 6cm,∠B = 100°);
ΔPQR;(PQ = 8cm,RP = 5cm,∠Q = 100°).
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.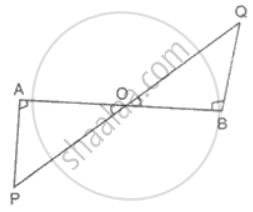
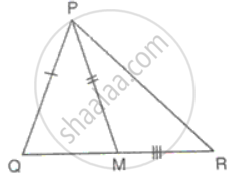
Sides, AB, BC and the median AD of ΔABC are equal to the two sides PQ, QR and the median PM of ΔPQR. Prove that ΔABC ≅ ΔPQR.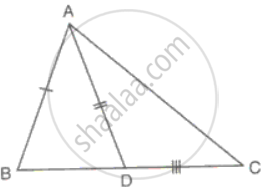
If AB = QR, BC = PR and CA = PQ, then ______.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆XYZ ≅ ∆MLN
