Advertisements
Advertisements
Question
If AB = QR, BC = PR and CA = PQ, then ______.
Options
∆ABC ≅ ∆PQR
∆CBA ≅ ∆PRQ
∆BAC ≅ ∆RPQ
∆PQR ≅ ∆BCA
Solution
If AB = QR, BC = PR and CA = PQ, then ∆CBA ≅ ∆PRQ.
Explanation:
We know that, if ΔRST is congruent to ΔUVW i.e., ΔRST = ΔUVW, then sides of ΔRST fall on corresponding equal sides of ΔUVW and angles of ΔRST fall on corresponding equal angles of ΔUVW.
Here, given AB = QR, BC = PR and CA = PQ, which shows that AB covers QR, BC covers PR and CA covers PQ i.e., A correspond to Q, B correspond to R and C correspond to P.
or A ↔ Q, B ↔ R, C ↔ P
Under this correspondence,
ΔABC ≅ ΔQRP, so option (a) is incorrect,
or ΔCBA ≅ ΔPRQ, so option (b) is correct,
or ΔBAC ≅ ΔRQP, so option (c) is incorrect,
or ΔBCA ≅ ΔRPQ, so option (d) is incorrect.
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(DF)`
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
If ΔABC ≅ ΔABC is isosceles with
Which of the following is not a criterion for congruence of triangles?
ABC is an isosceles triangle such that AB = AC and AD is the median to base BC. Then, ∠BAD =
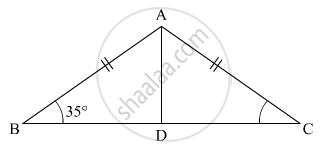
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

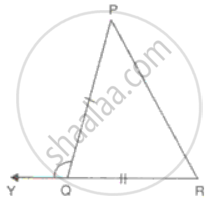
In ΔABC and ΔPQR and, AB = PQ, BC = QR and CB and RQ are extended to X and Y respectively and ∠ABX = ∠PQY. = Prove that ΔABC ≅ ΔPQR.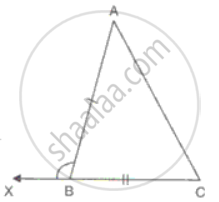
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
