Advertisements
Advertisements
प्रश्न
If AB = QR, BC = PR and CA = PQ, then ______.
पर्याय
∆ABC ≅ ∆PQR
∆CBA ≅ ∆PRQ
∆BAC ≅ ∆RPQ
∆PQR ≅ ∆BCA
उत्तर
If AB = QR, BC = PR and CA = PQ, then ∆CBA ≅ ∆PRQ.
Explanation:
We know that, if ΔRST is congruent to ΔUVW i.e., ΔRST = ΔUVW, then sides of ΔRST fall on corresponding equal sides of ΔUVW and angles of ΔRST fall on corresponding equal angles of ΔUVW.
Here, given AB = QR, BC = PR and CA = PQ, which shows that AB covers QR, BC covers PR and CA covers PQ i.e., A correspond to Q, B correspond to R and C correspond to P.
or A ↔ Q, B ↔ R, C ↔ P
Under this correspondence,
ΔABC ≅ ΔQRP, so option (a) is incorrect,
or ΔCBA ≅ ΔPRQ, so option (b) is correct,
or ΔBAC ≅ ΔRQP, so option (c) is incorrect,
or ΔBCA ≅ ΔRPQ, so option (d) is incorrect.
APPEARS IN
संबंधित प्रश्न
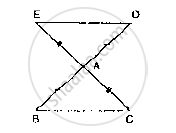
In Fig. 10.22, the sides BA and CA have been produced such that: BA = AD and CA = AE.
Prove that segment DE || BC.
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that: LN = MN.
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.
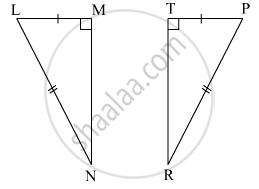
By ______ test
ΔLMN ≅ ΔPTR
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
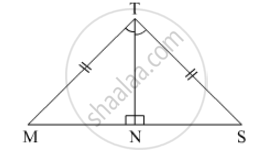
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.

If the following pair of the triangle is congruent? state the condition of congruency :
In ΔABC and ΔDEF, ∠B = ∠E = 90o; AC = DF and BC = EF.
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

In ΔABC, AB = AC, BM and Cn are perpendiculars on AC and AB respectively. Prove that BM = CN.
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.
