Advertisements
Advertisements
प्रश्न
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

उत्तर
In ΔABC, AB = AC. m and N are points on
AB and AC such that BM = CN
BN and CM are joined

(i) The corresponding parts of the congruent triangles are congruent.
∴ CM = BN ....[ c.p.c.t ] ...(1)
(ii) Consider the triangles ΔBMC and ΔCNB
BM = CN ...[ given ]
BC = BC ...[ common ]
Cm = BN ..[ from (1) ]
∴ By Side-Side-Side criterion of congruence, we have ΔBMC ≅ ΔCNB
APPEARS IN
संबंधित प्रश्न
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
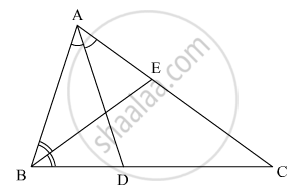
In the given figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that ADbisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
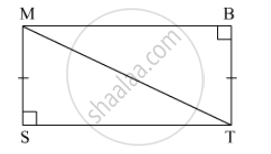
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
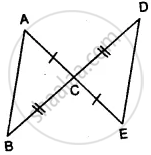
State, whether the pairs of triangles given in the following figures are congruent or not:
Δ ABC in which AB = 2 cm, BC = 3.5 cm and ∠C = 80° and Δ DEF in which DE = 2 cm, DF = 3.5 cm and ∠D = 80°.
In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
In the figure, ∠CPD = ∠BPD and AD is the bisector of ∠BAC. Prove that ΔCAP ≅ ΔBAP and CP = BP.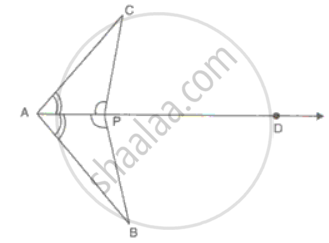
In the figure, AB = EF, BC = DE, AB and FE are perpendiculars on BE. Prove that ΔABD ≅ ΔFEC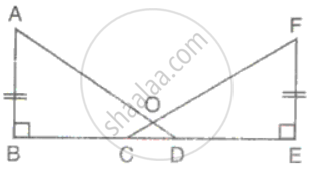
In the figure, RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.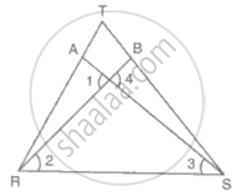
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
