Advertisements
Advertisements
प्रश्न
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
उत्तर
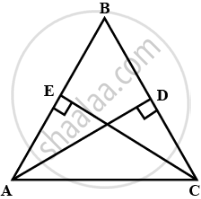
ln ΔABD and ΔCBE,
AB = BC ....(given)
AD ⊥ BC
CE ⊥ AB
To proved:
In ΔABD & ΔCBE
∠ ADB = ∠ CEB = 90° ....[Perpendiculars]
∠B = ∠B ....(Common angle)
AB = BC
∴ ΔABD ≅ ΔCBE ....(by AAS congruence)
⇒ AD = CE ...(c.p.c.t.c)
APPEARS IN
संबंधित प्रश्न
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

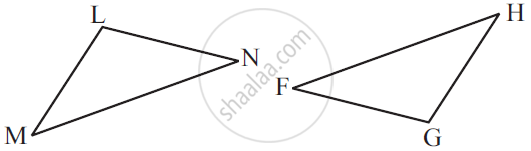
Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
ABCD is a square, X and Yare points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
