Advertisements
Advertisements
प्रश्न
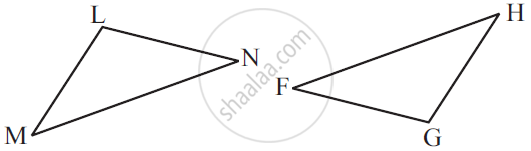
Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
उत्तर
ASA, as two angles and the side included between these angles of ΔLMN are equal to two angles and the side included between these angles of ΔGFH.
APPEARS IN
संबंधित प्रश्न
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

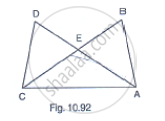
In Fig. 10.92, it is given that AB = CD and AD = BC. Prove that ΔADC ≅ ΔCBA.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
