Advertisements
Advertisements
प्रश्न
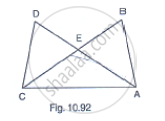
In Fig. 10.92, it is given that AB = CD and AD = BC. Prove that ΔADC ≅ ΔCBA.
उत्तर
Given that in the figure AB =CD and . AD=BC
We have to prove
ΔADC≅ΔCBA
Now,
Consider ΔADC and ΔCBA
We have
AB = CD [Given]
BC = AD [Given]
And AC=AC [Common side]
So, by SSS congruence criterion, we have
ΔADC≅ΔCBA
∴ Hence proved
APPEARS IN
संबंधित प्रश्न
You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
Which of the following is not a criterion for congruence of triangles?
