Advertisements
Advertisements
प्रश्न
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
उत्तर
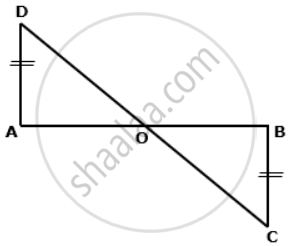
In ΔAOD and ΔBOC,
∠ AOD = ∠ BOC ....(vertically opposite angles)
∠ DAO = ∠ CBO ....(each 90°)
AD = BC ....(given)
∴ ΔAOD ≅ ΔBOC ...(by AAS congruence criterion)
⇒ AO = BO ...(c.p.c.t.)
⇒ O is the mid-point of AB.
Hence, CD bisects AB.
APPEARS IN
संबंधित प्रश्न
Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

In the given figure, AB = DB and Ac = DC.
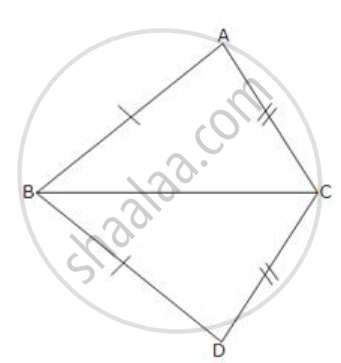
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
