Advertisements
Advertisements
प्रश्न
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
उत्तर
In ΔDLB and ΔDMC,
BL = CM ...( given )
∠DLB = ∠DMC ...( Both are 90° )
∠BDL = ∠CDM ....( vertically opposite angels )
∴ ΔDLB ≅ ΔDMC ....( AAS congruence criterion )
BD = CD ....( cpct )
Hence, AD is the median of ΔABC.
APPEARS IN
संबंधित प्रश्न
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =

In the figure, the two triangles are congruent.
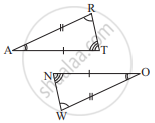
The corresponding parts are marked. We can write ΔRAT ≅ ?
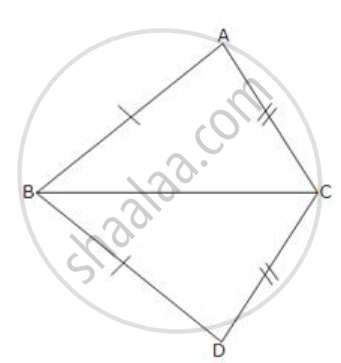
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
In the given figure, AB = DB and Ac = DC.
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS ⊥ QR and XT ⊥ PQ ;
prove that: (i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
