Advertisements
Advertisements
प्रश्न
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
उत्तर
For the triangles ABC and ECD, we have the following information and corresponding figure:
AC = CE
BC = CD
∠A = 60°
∠C = 30°
∠D = 90°
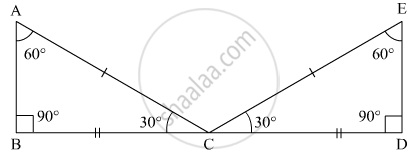
In triangles ABC and ECD, we have
AC = EC
BC = CD
and ∠BAC= ∠CED
The SSA criteria for two triangles to be congruent are being followed. So both the triangles are congruent.
APPEARS IN
संबंधित प्रश्न
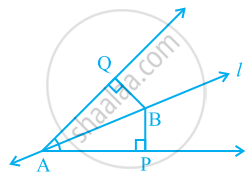
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
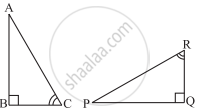
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
In the given figure, AB = DB and Ac = DC.
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
