Advertisements
Advertisements
प्रश्न
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
उत्तर
Given: in the figure, O is center of the circle, and AB is chord. P is a point on AB such that AP = PB.
We need to prove that, OP ⊥ AB
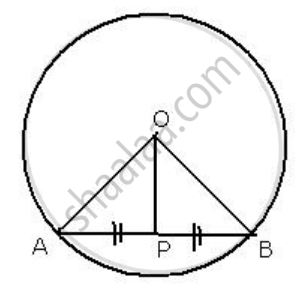
Construction: Join OA and OB
Proof:
In ΔOAP and ΔOBP
OA = OB ...[radii of the same circle]
OP = OP ...[common]
AP = PB ...[given]
∴ By Side-Side-Side criterion of congruency,
ΔOAP ≅ ΔOBP
The corresponding parts of the congruent triangles are congruent.
∴ ∠OPA = ∠OPB ...[by c.p.c.t]
But ∠OPA + ∠OPB = 180° ...[linear pair]
∴ ∠OPA = ∠OPB = 90°
Hence OP ⊥ AB.
APPEARS IN
संबंधित प्रश्न
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
In the given figure, prove that:
CD + DA + AB + BC > 2AC

In the given figure, prove that:
CD + DA + AB > BC
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
