Advertisements
Advertisements
प्रश्न
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, BC = QR, ∠A = 90°, ∠C = ∠R = 40° and ∠Q = 50°.
उत्तर
In ΔPQR
∠R = 40°, ∠Q = 50°
∠P + ∠Q + ∠R = 180° ...[Sum of all the angels in aa triangle = 180°]
⇒ ∠P + 50° + 40° = 180°
⇒ ∠P + 90° = 180°
⇒ ∠P = 180° - 90°
⇒ ∠P = 90°
In ΔABC and ΔPQR
∠A = ∠P
∠C = ∠R
BC = QR

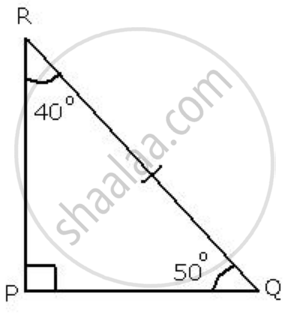
By Angle-Angle-Side criterion of congruency, the triangles
ΔABC and ΔPQR are congruent to each other.
∴ ΔABC ≅ ΔPQR
APPEARS IN
संबंधित प्रश्न
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that: LN = MN.
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
In the given figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
Which of the following is not a criterion for congruence of triangles?
In the given figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that ADbisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
The congruent figures super impose each other completely.
