Advertisements
Advertisements
Question
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, BC = QR, ∠A = 90°, ∠C = ∠R = 40° and ∠Q = 50°.
Solution
In ΔPQR
∠R = 40°, ∠Q = 50°
∠P + ∠Q + ∠R = 180° ...[Sum of all the angels in aa triangle = 180°]
⇒ ∠P + 50° + 40° = 180°
⇒ ∠P + 90° = 180°
⇒ ∠P = 180° - 90°
⇒ ∠P = 90°
In ΔABC and ΔPQR
∠A = ∠P
∠C = ∠R
BC = QR

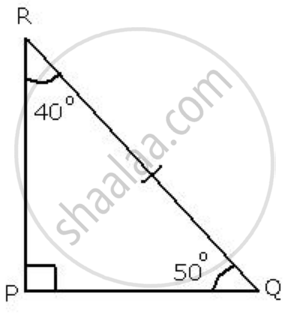
By Angle-Angle-Side criterion of congruency, the triangles
ΔABC and ΔPQR are congruent to each other.
∴ ΔABC ≅ ΔPQR
APPEARS IN
RELATED QUESTIONS
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that: LN = MN.
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
In triangles ABC and PQR three equality relations between some parts are as follows:
AB = QP, ∠B = ∠P and BC = PR
State which of the congruence conditions applies:
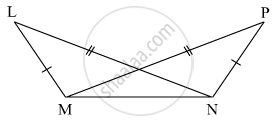
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

State, whether the pairs of triangles given in the following figures are congruent or not:

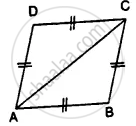
Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
In the figure, ∠BCD = ∠ADC and ∠ACB =∠BDA. Prove that AD = BC and ∠A = ∠B.
“If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
