Advertisements
Advertisements
Question
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, AB = PQ, AC = PR, and BC = QR.
Solution
In ΔABC and ΔPQR
AB = PQ ...[Given]
AC = PR ...[Given]
BC = QR ...[Given]
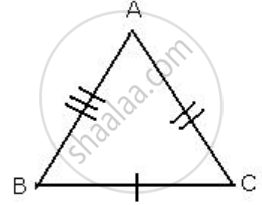
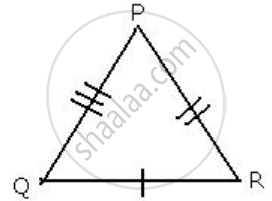
By Side-Side-Side criterion of congruency, the triangles
ΔABC and ΔPQR are congruent to each other.
∴ ΔABC ≅ ΔPQR
APPEARS IN
RELATED QUESTIONS
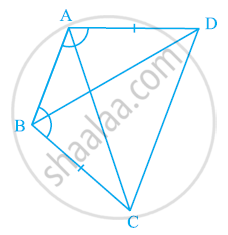
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
- ΔABD ≅ ΔBAC
- BD = AC
- ∠ABD = ∠BAC.
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

You want to show that ΔART ≅ ΔPEN,
If it is given that AT = PN and you are to use ASA criterion, you need to have
1) ?
2) ?

If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
