Advertisements
Advertisements
Question
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
Solution
We have to prove that the perimeter of a triangle is greater than the sum of its altitude.
In ΔABC
AD⊥ BC , BE ⊥ AC , CF⊥AB

We have to prove
AB + BC + CD > AD + BE + CF
Since AD⊥ BC
So AB > AD and AC > AD
By adding AB + AC > AD + AD, we have
AB + AC > 2AD ........(1)
Now consider BE ⊥ AC then
BC > BE, and BA > BE
Now by adding BC + BA > 2BE .......(2)
Again consider CF⊥AB
AC > CF, and BC > CF
By adding AC + BC > 2CF ...........(3)
Adding (1), (2) and (3), we get
2(AB + BC + CA)>2 (AD + BE + CF)
⇒ AB + BC + CA > AD + BE + CF
Hence the perimeter of a triangle is greater than the sum of all its altitude.
APPEARS IN
RELATED QUESTIONS
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
In the given figure, AB = DB and Ac = DC.
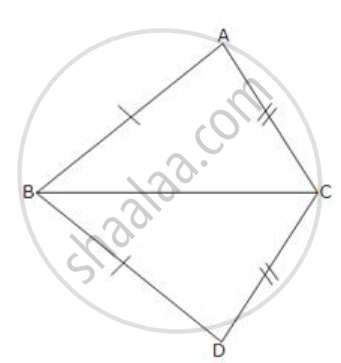
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
