Advertisements
Advertisements
Question
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

Solution
In △BOC and △AOD,
∠OBC = ∠OAD ...[Each 90° (Given)]
∠BOC = ∠AOD ...[Vertically opposite angles]
BC = AD ...[Given]
∴ △BOC ≌ △AOD ...[By AAS congruence rule]
⇒ OB = OA ...[Corresponding parts of congruent triangles]
i.e., O is the mid-point of AB.
So, CD bisects the line segment AB.
APPEARS IN
RELATED QUESTIONS
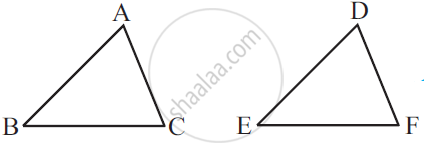
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

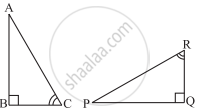
If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
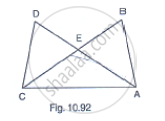
In Fig. 10.92, it is given that AB = CD and AD = BC. Prove that ΔADC ≅ ΔCBA.
In the given figure, prove that:
CD + DA + AB + BC > 2AC

In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
Use the information in the given figure to prove:
- AB = FE
- BD = CF

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, AB = PQ, AC = PR, and BC = QR.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
