Advertisements
Advertisements
Question
Use the information in the given figure to prove:
- AB = FE
- BD = CF

Solution
ln ΔABC and ΔEFD,
AB II EF
⇒ ∠ABC = ∠EFD ...(alternate angles)
AC = ED ...(given)
∠ACB = ∠EDF ...(given)
∴ ΔABC ≅ ΔEFD ...(AAS congruence criterion)
⇒ AB = FE ...(cpct)
and BC = DF ...(cpct)
⇒ BD + DC = CF + DC ...(B-D-C-F)
⇒ BD = CF
APPEARS IN
RELATED QUESTIONS
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
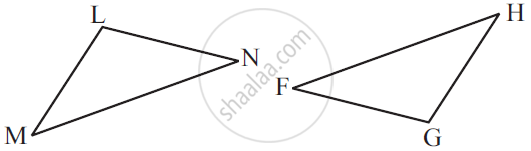
In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
