Advertisements
Advertisements
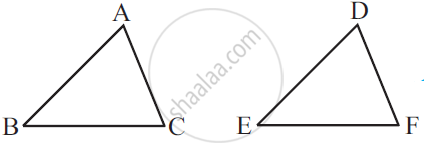
प्रश्न
Use the information in the given figure to prove:
- AB = FE
- BD = CF

उत्तर
ln ΔABC and ΔEFD,
AB II EF
⇒ ∠ABC = ∠EFD ...(alternate angles)
AC = ED ...(given)
∠ACB = ∠EDF ...(given)
∴ ΔABC ≅ ΔEFD ...(AAS congruence criterion)
⇒ AB = FE ...(cpct)
and BC = DF ...(cpct)
⇒ BD + DC = CF + DC ...(B-D-C-F)
⇒ BD = CF
APPEARS IN
संबंधित प्रश्न
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
D, E, F are the mid-point of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
