Advertisements
Advertisements
प्रश्न
Use the information in the given figure to prove:
- AB = FE
- BD = CF

उत्तर
ln ΔABC and ΔEFD,
AB II EF
⇒ ∠ABC = ∠EFD ...(alternate angles)
AC = ED ...(given)
∠ACB = ∠EDF ...(given)
∴ ΔABC ≅ ΔEFD ...(AAS congruence criterion)
⇒ AB = FE ...(cpct)
and BC = DF ...(cpct)
⇒ BD + DC = CF + DC ...(B-D-C-F)
⇒ BD = CF
APPEARS IN
संबंधित प्रश्न
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

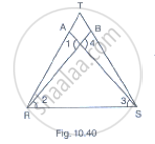
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
ABCD is a square, X and Yare points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
