Advertisements
Advertisements
प्रश्न
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
उत्तर
Given: A(ΔABC) in which BD is the median to AC.
BD is produced to E such that BD = DE,
We need to prove that AE II BC.
Construction: Join AE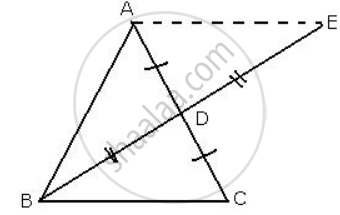
Proof:
AD = DC ...[ BD is median to AC ] ...(1)
In ΔBDC and ΔADE,
BD = DE ...[ Given ]
∠BDC = ∠ADE = 90° ...[ Vertically opposite angles ]
AD = DC ...[ from(1) ]
∴ By Side-Angle-Side Criterion of congruence,
ΔBDC ≅ ΔADE
The corresponding parts of the congruent triangles are congruent.
∴ ∠EAD = ∠BCD ...[ c.p.c.t. ]
But these are alternate angles and AC is the transversal.
Thus, AE || BC.
APPEARS IN
संबंधित प्रश्न
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

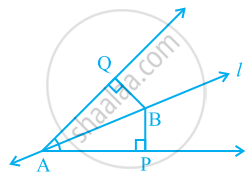
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°.
Prove that AD = FC.
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
