Advertisements
Advertisements
प्रश्न
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS ⊥ QR and XT ⊥ PQ ;
prove that: (i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
उत्तर
Given: A( ΔPQR ) in which QX is the bisector of ∠Q. and RX is the bisector of ∠R.
XS ⊥ QR and XT ⊥ PQ.
We need to prove that
(i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
Construction: Draw XZ ⊥ PR and join PX.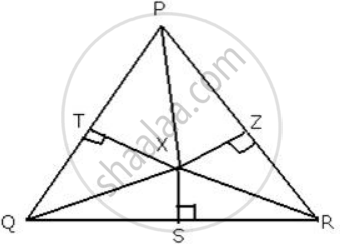
Proof:
(i) In ΔXTQ and ΔXSQ,
∠QTX = ∠QSX = 90° ...[ XS ⊥ QR and XT ⊥ PQ ]
∠TQX = ∠SQX ...[ QX is bisector of ∠Q ]
QX = QX ...[ Common ]
∴ By Angle-Side-Angle Criterion of congruence,
ΔXTQ ≅ ΔXSQ
(ii) The corresponding parts of the congruent triangles are congruent.
∴ XT = XS ...[ c.p.c.t. ]
In ΔXSR & ΔXRZ
∠XSR = ∠XZR = 90° ...[ XS ⊥ QR and ∠XSR = 90° ]
∠XRS = ∠ZRX ...[ RX is bisector of ∠R ]
RX = RX ....[ Common ]
∴ By Angle-Angle-Side criterion of congruence,
ΔXSR ≅ ΔXRZ
The corresponding parts of the congruent triangles are congruent.
∴ XS = XT ...[ c.p.c.t. ]
From (1) and (2)
XT = XZ
In ΔXTP and ΔPZX
∠XTP = ∠XZP = 90° ....[ Given ]
XP = XP ....[ Common ]
XT = XZ
∴ By Right angle-Hypotenuse-side criterion of congruence,
ΔXTP ≅ ΔPZX
The corresponding parts of the congruent triangles are
congruent.
∴ ∠TPX = ∠ZPX ...[ c.p.c.t. ]
∴ PX bisects ∠P.
APPEARS IN
संबंधित प्रश्न
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
